Introduction
Geocache puzzles are varied, and as befitting a game enjoyed by geeks many geocaches can only be found after you’ve solved a geeky puzzle. Some such puzzles involve electronics, and within this niche we find those which involve digital logic.
I’ve solved about half-a-dozen of them, and even set one: GC40ZBM1 near Cambridge in the UK.
A puzzle
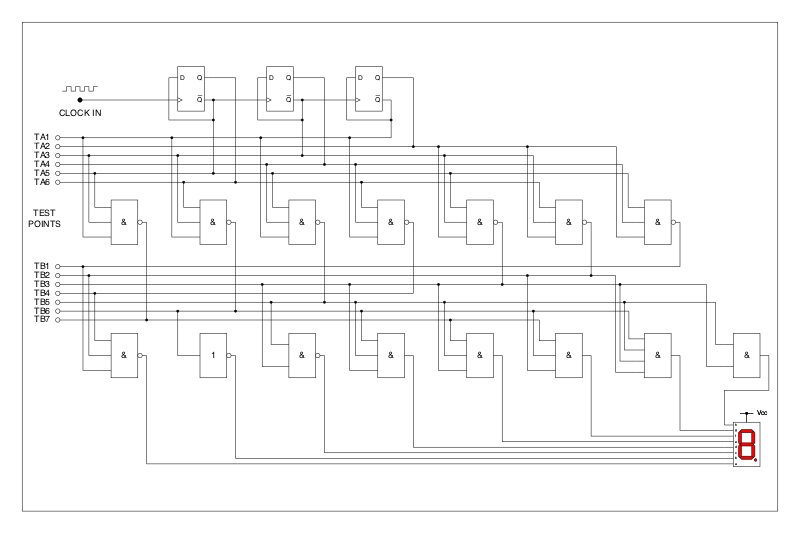
To make things more concrete, consider the following circuit:
After some deliberation you might realize that the seven-segment display shows the sequence N, 5, 2, 1, 2, 4, 1, 7 which you might recognize as the Northing of the Great Court3 Fountain.
Solving the problem by hand isn’t difficult: the circuit is structured to make manual simulation easy, and the task is guided by the test points shown on the left-hand side of the schematic.
However it’s always nice to make things with flashing lights, I had a iCE40 FPGA demo board on my desk, and this seemed worth a try:

More LEDs!
The FPGA has many pins, so it seemed a shame to drive only a single digit:

Verilog
Converting the schematic to verilog wasn’t hard, though there’s an off-by-one error somewhere which I bodged around.
The code below only covers the elements shown in the schematic, you need a bit more the generate the input clock and wire things up.
module puzzle(input clk
, input rst
, output [5:0] ta
, output [7:0] tb
, output [7:0] seg
, output [7:0] dig);
wire [2:0] qs;
counter c1 (.clk(clk), .rst(rst), .qs(qs));
gates gs (.q(qs), .ta(ta), .tb(tb), .seg(seg));
digits ds (.notSel(tb), .digs(dig));
endmodule
module counter(input clk, input rst, output [2:0] qs);
reg q0, q1, q2;
always @(posedge clk)
q0 <= (rst) ? 0 : !q0;
always @(posedge !q0)
q1 <= (rst) ? 0 : !q1;
always @(posedge !q1)
q2 <= (rst) ? 0 : !q2;
wire [2:0] qs;
assign qs = {q2, q1, q0};
endmodule
module digits(input [7:0] notSel,
output [7:0] digs);
// odd offset here!
assign digs[0] = (notSel[6]) ? 0 : 1;
assign digs[1] = (notSel[5]) ? 0 : 1;
assign digs[2] = (notSel[4]) ? 0 : 1;
assign digs[3] = (notSel[3]) ? 0 : 1;
assign digs[4] = (notSel[2]) ? 0 : 1;
assign digs[5] = (notSel[1]) ? 0 : 1;
assign digs[6] = (notSel[0]) ? 0 : 1;
assign digs[7] = (notSel[7]) ? 0 : 1;
endmodule
module gates(input [2:0] q,
output [5:0] ta,
output [7:0] tb,
output [7:0] seg);
assign ta[0] = !q[2];
assign ta[1] = q[2];
assign ta[2] = !q[1];
assign ta[3] = q[1];
assign ta[4] = !q[0];
assign ta[5] = q[0];
assign tb[0] = !(ta[1] & ta[3] & ta[5]);
assign tb[1] = !(ta[1] & ta[3] & ta[4]);
assign tb[2] = !(ta[1] & ta[2] & ta[5]);
assign tb[3] = !(ta[1] & ta[2] & ta[4]);
assign tb[4] = !(ta[0] & ta[3] & ta[5]);
assign tb[5] = !(ta[0] & ta[3] & ta[4]);
assign tb[6] = !(ta[0] & ta[2] & ta[5]);
assign tb[7] = !(ta[0] & ta[2] & ta[4]);
assign seg[0] = !(tb[0] & tb[1] & tb[3]);
assign seg[1] = !tb[5];
assign seg[2] = !(tb[2] & tb[4]);
assign seg[3] = tb[2] & tb[4] & tb[5];
assign seg[4] = tb[2] & tb[4] & tb[6];
assign seg[5] = tb[1] & tb[5] & tb[6];
assign seg[6] = tb[1] & tb[2] & tb[4] & tb[5];
assign seg[7] = tb[2] & tb[4];
endmodule Conclusion
So there you have it. This isn’t a particularly good way to solve the puzzle but it didn’t take long and has an impressive blinkenlight4 score.
References
- 1. https://www.geocaching.com/geocache/GC40ZBM_digital-electronics-theory?guid=533d0f0b-d247-4a8b-a5fa-b5c56f50fe6b
- 2. ./trin.pdf
- 3. https://en.wikipedia.org/wiki/Trinity_Great_Court
- 4. https://en.wikipedia.org/wiki/Blinkenlights


![Atom Feed [ Atom Feed ]](../../atom.png)