Introduction
Recently I wrote about arranging magnets to hold geocaches onto magnetic objects. In particular, given a couple of magnets should their dipoles be aligned so as to be parallel, or anti-parallel ?
The simple dipole model I used there suggested that it anti-parallel would be a bit better, but not significantly so. However, given that this arrangement is much easier to make, there wasn’t a conflict and so the conclusion was clear.
Experiments
Of course, the physicist in me wanted to know whether reality matched the model, and that means an experiment. So, I made some little acrylic holders then measured how much weight they’d support when attracted to a 40mm square mild-steel beam.
The table below shows the results: the mass of the maximum weight the magnets could support in different orientations. Two different pairs of magnets were used.
| Pair | Orientation | Difference | |
|---|---|---|---|
| Parallel | Anti-parallel | ||
| A | 1.6kg | 2.0kg | 22% |
| B | 1.45kg | 1.7kg | 16% |
N.B. Difference = 2 (max - min) / (max + min)
The experiment was crude, and it was hard to get consistent readings, but the conclusion is still clear: the anti-parallel arrangement is indeed better, and by a significant margin!
To quantify the imprecision I expect the measurements have an uncertainty of about 100g.
There also seemed to be some preferred spots on the bar which makes me wonder if it was being magnetized to some degree.
Nevertheless, despite the having so few data and the rather crude experiment, it seems clear that the simple model does a poor job of capturing reality.
The old model
Formally, it can be shown (or looked up in Wikipedia1) that the force between two dipoles \(\textbf{m}_1\) and \(\textbf{m}_2\) a distance \(\textbf{r}\) apart is given by
\[ \textbf{F} = \frac{3 \mu_0}{4 \pi r^4} \Bigl( (\hat{\textbf{r}} \times \textbf{m}_1 ) \times \textbf{m}_2 + (\hat{\textbf{r}} \times \textbf{m}_2 ) \times \textbf{m}_1 - 2 \, \hat{\textbf{r}} \, (\textbf{m}_1 . \textbf{m}_2) + 5 \, \hat{\textbf{r}} \, \bigl((\hat{\textbf{r}} \times \textbf{m}_1) . (\hat{\textbf{r}} \times \textbf{m}_2)\bigr) \Bigr). \]In our case the dipoles are both in the \(z\) direction, and we are interested in the \(z\)-component of the force. Writing
\[ \begin{align} \textbf{r} &= (x,y,z), \\\ \textbf{m}_1 &= (0,0,m), \\\ \textbf{m}_2 &= (0,0,m), \end{align} \]it is a matter of algebra to show that,
\[ F_z = \frac{3 \mu m^2}{4 \pi} \, \frac{z(3x^2 + 3y^2 - 2z^2)}{(x^2 + y^2 + z^2)^{7/2}}. \]Now, recall this diagram from the previous article and calculate the force on the dipole at A due to the dipoles at A', and B'.
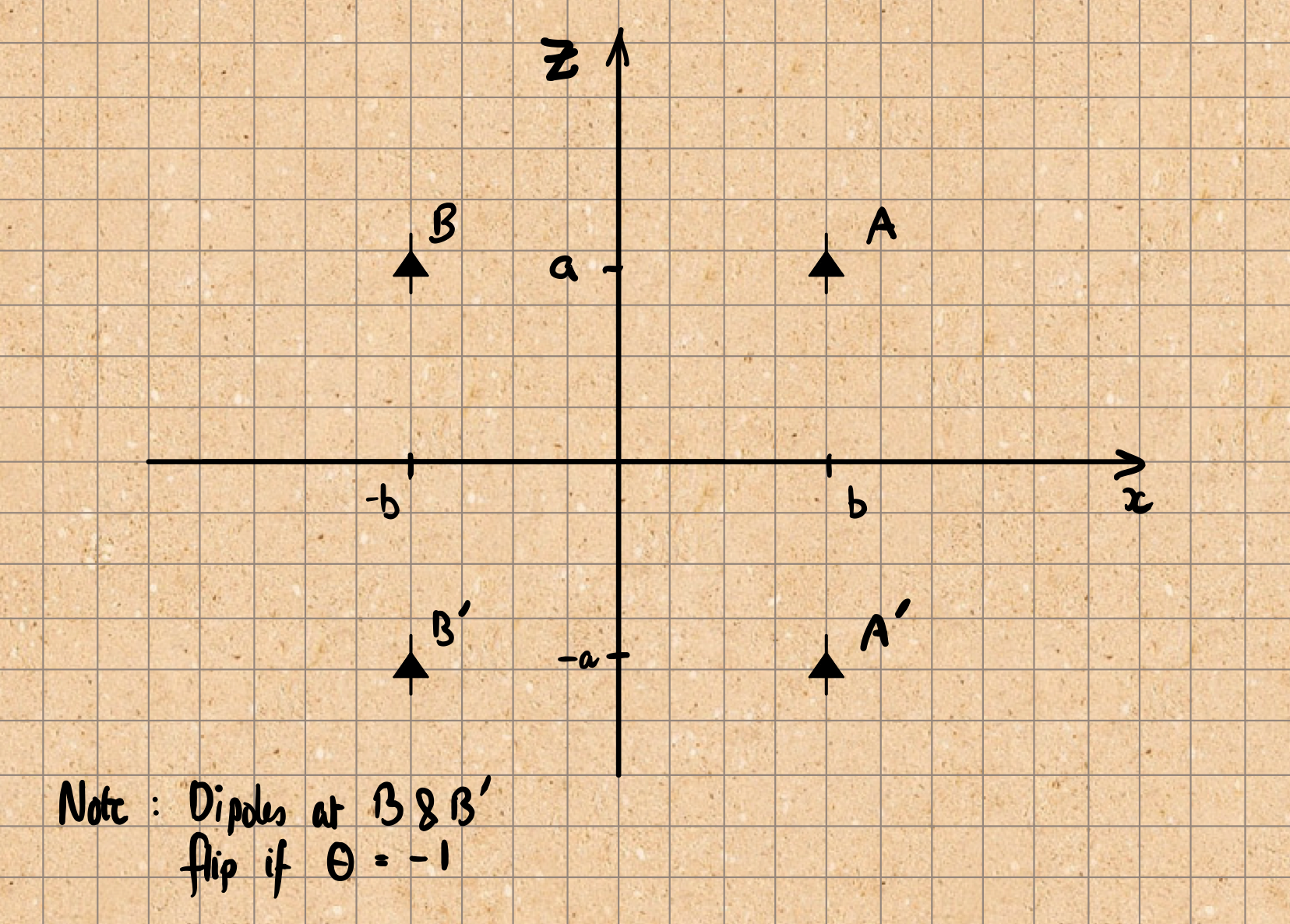
Now, the magnetic adhesion force is given by
\[ F_{tot} = 2 \bigl( F_z(A') + \theta F_z(B') \bigr), \]where \(\theta\) encodes the relative orientation of the dipoles. and the prefactor of two comes from including the force on B too.
Finally, to calculate the difference between the parallel and anti-parallel alignments we need
\[ \begin{align} \chi &= 2 \frac{F_{tot}(\theta = -1) - F_{tot}(\theta = +1)}{F_{tot}(\theta = -1) + F_{tot}(\theta = +1)},\\\ &= -2 \frac{F_z(B')}{F_z(A')},\\\ &= \frac{a^5(3 b^2 - 2 a^2)}{(a^2 + b^2)^{7/2}}. \end{align} \]Substituting \(a = 1.5\textrm{mm}\), \(b = 5\textrm{mm}\) into this gives
\[ \chi \approx 0.005. \]Happily, this is in agreement with the previous result (the factor of two comes from a different measure of difference).
In the actual experiment there’s a 1mm thick sheet of acrylic between the magnet and the bar so it’s more appropriate to use \(a = 2.5\textrm{mm}, b = 5\textrm{mm}\):
this gives
\[ \chi \approx 0.036. \]A better model
The original model represented each magnet by a dipole at its centre. So, an obvious improvement would be to assume that the magnet is made up of a continuum of dipoles arranged uniformly.
Mathematically we need to replace \(F_z\) with integrals over the volume of the magnets:
\[ \begin{align} G_z &= \int_{V1} \textrm{d}V_1 \int_{V2} \textrm{d}V_2 F_z \\\ &= \frac{3 \mu \sigma^2}{4 \pi} \int_{V1} \textrm{d}V_1 \int_{V2} \textrm{d}V_2 \frac{z(3x^2 + 3y^2 - 2z^2)}{(x^2 + y^2 + z^2)^{7/2}}. \end{align} \]where we’ve replaced the dipole moment \(m\) with a density \(\sigma\).
Introduce cylindrical polars to integrate over the magnets and assume the magnet centres are offset by \((u,v,w)\) to give:
\[ \begin{align} x &= u + \rho_2 \cos\theta_2 - \rho_1 \cos\theta_1, \\\ y &= v + \rho_2 \sin\theta_2 - \rho_1 \sin\theta_1, \\\ z &= w + \tau_2 - \tau_1. \end{align} \]and thus, if the magnets have thickness \(t\) and radius \(s\):
\[ \int_{V} \textrm{d}V \equiv \int_0^s \int_0^{2\pi} \int_{-t/2}^{t/2} \rho \, \textrm{d}\tau \, \textrm{d}\theta \, \textrm{d}\rho, \]An analytic result seems optimistic, so let’s ask Mathematica to do the calculation numerically. We are only interested in the ratio of forces, so I’ve dropped the prefactor.
Fz[{x_, y_, z_}] :=
z * (3 x^2 + 3 y^2 - 2 z^2) / (x^2 + y^2 + z^2)^(7/2)Checking with the result above for \(a = 2.5\textrm{mm}, b = 5\textrm{mm}\) and recalling that e.g. \(w = 2a\),
In[]:= -2 * N[Fz[{10, 0, 5}] / Fz[{0, 0, 5}]]
Out[]= 0.0357771Now define the integral:
Gz[s_, t_, {u_, v_, w_}] :=
NIntegrate[
Fz[{u + \[Rho]2 * Cos[\[Theta]2] - \[Rho]1 * Cos[\[Theta]1],
v + \[Rho]2 * Sin[\[Theta]2] - \[Rho]1 * Sin[\[Theta]1],
w + \[Tau]2 - \[Tau]1}],
{\[Tau]1, -t/2, t/2},
{\[Tau]2, -t/2, t/2},
{\[Theta]1, 0, 2 * Pi},
{\[Theta]2, 0, 2 * Pi},
{\[Rho]1, 0, s},
{\[Rho]2, 0, s},
Method -> "AdaptiveMonteCarlo"]If we use this to model the simple dipole case by setting \(s = 0.1\) and \(t = 0.1\), we get \(\chi \approx 0.03586\) which agrees well with the true simple dipole result of \(\chi \approx 0.03578\):
In[]:= -2 * Gz[0.1, 0.1, {10, 0, 5}] / Gz[0.1, 0.1, {0, 0, 5}]
Out[]= 0.0358565Substituting the true magnet size \(s = 5\textrm{mm}, t = 3\textrm{mm}\) and positions \(a = 2.5\textrm{mm}, b = 5\textrm{mm}\), gives
In[]:= -2 * Gz[5, 3, {10, 0, 5}] / Gz[5, 3, {0, 0, 5}]
Out[]= 0.152685which agrees pretty well with the experiment: 15% for theory vs 16-22% from experiment.
Discussion
As noted above it’s hard to measure the maximum weight the magnets will support, so I’d be wary of saying anything stronger than difference is between 14% and 25%.
Our theoretical result is similar but probably a little on the small side. We’ve also assumed that the magnets are equally strong, which seems a bit optimistic. Any imbalance will reduce the difference. Thus, the experimental value is probably still a bit larger than this model predicts.
One potential contribution is that when the dipoles are aligned in parallel, they really want to stagger themselves. The diagram below sketches equilibrium arrangements for magnets lying on a non-magnetic surface, where the magnets are constrained to lie in roughly the same plane.
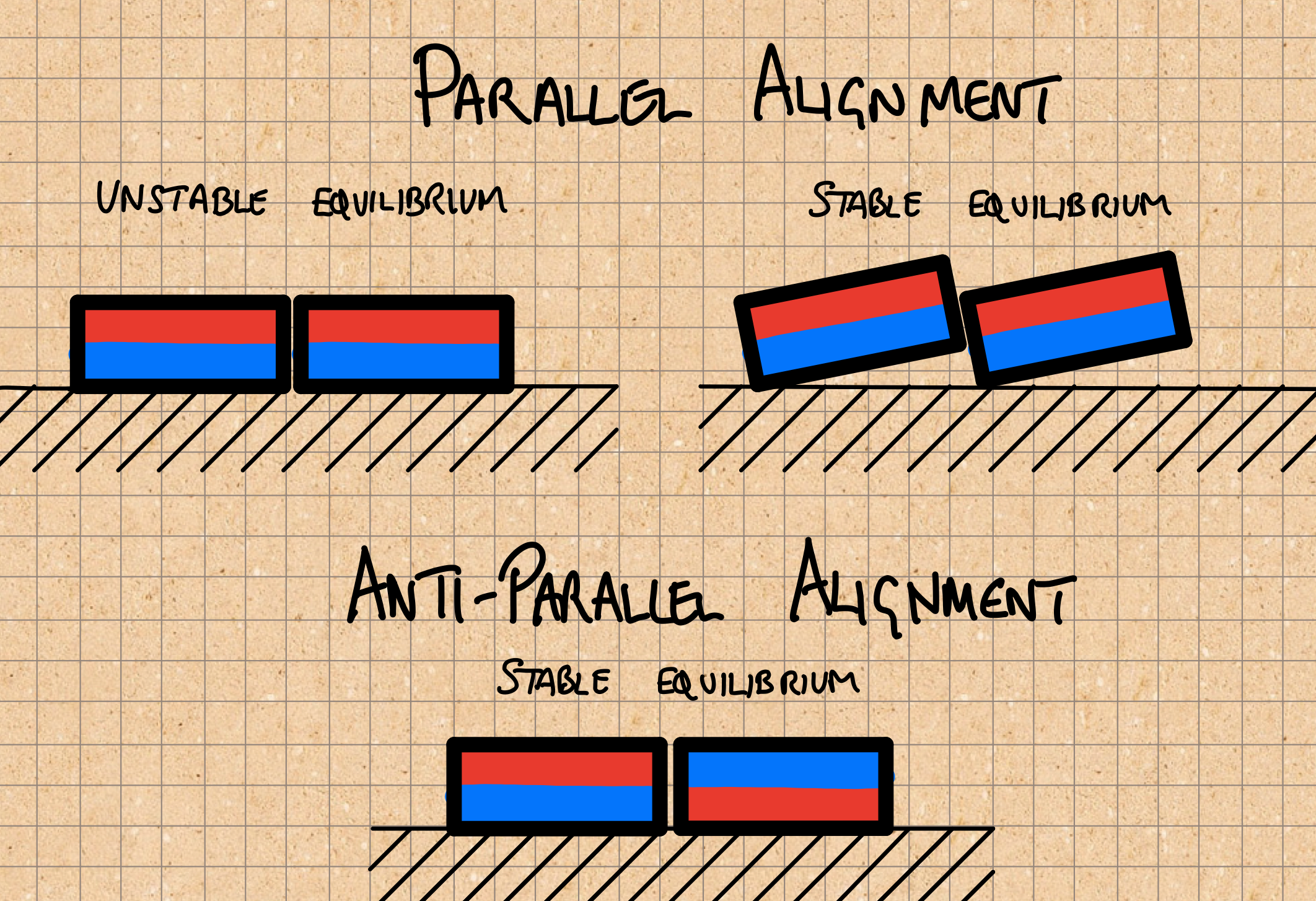
If this happens, then in the parallel case the magnets will be a bit further from the bar and thus be held less strongly.
Quantifying this is hard: you’d need to model the way the thin sheet of perspex flexs, or find a way to hold the magnets to prevent the movement: probably glue!
I also have some concerns that the bar becomes magnetized, which is obviously outside the scope of the model.
Conclusions
This whole project started because I was curious about how best to arrange a pair of magnets on a geocache, and that’s now answered to my satisfaction. Just do the easy thing and align their dipoles to be anti-parallel.
Another lesson is that it’s fairly easy to tackle numerical solutions to this sort of thing in Mathematica.
Finally, and perhaps most germane to the geocache question it is nice to know that a couple of small magents can hold a bison tube firmly enough to a steel bar that you can hang well over a kilogramme from it!
References
- 1. https://en.wikipedia.org/wiki/Magnetic_dipole–dipole_interaction


![Atom Feed [ Atom Feed ]](../../atom.png)