Recently I wrote about making magnetic bison tubes1: little aluminum geocaches which stick to iron and steel by virtue of having two disc magnets attached to them.
When I made these, I arranged the magnets in opposite senses so that they stick together. This makes it easier to assemble the geocaches, but I wondered if such expediency led to inferior sticking force.
In other words, in the sketch below, which of the green geocaches is held more strongly to the metal ?
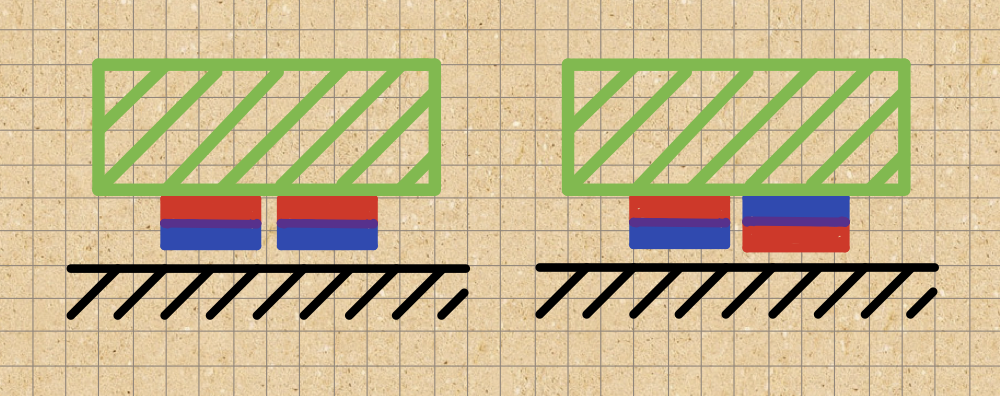
Is it the geocache on the left where the magnets have the same polarity, or the one on the right where they point in opposite directions ?
To answer this, let’s build a simple model.
One magnet
Perhaps the simplest possible model for a magnet sticking to a flat metal surface is to assume that:
- The magnet is well represented by a simple dipole, perpendicular to the metal surface.
- The metal is sufficiently thick to be well represented by a half-space e.g. \(y < 0\).
- Magnetically the metal has a high relative-permeability \(\mu >> 1\), but we can neglect any intrinsic magnetization.
This last point is perhaps dodgy: we are effectively saying that the ‘metal’ is paramagnetic but has a permeability typical of a ferromagnet.
Such problems, particularly in electrostatics, are conveniently solved by the method of image-charges2. The image-charge trick is to combine solutions which don’t satisfy the boundary conditions into one which does. We can do this because Maxwell’s equations are all linear in the fields, so any combination of solutions is also a solution.
Now, although magnetic monopoles do not exist, they are useful for calculations. For example, we can represent a dipole as two monopoles with opposite charges slightly displaced from each other. To find the image of the dipole, we need to only to superimpose the images of the two monopoles.
That just leaves the problem of finding the image of a magnetic monopole above a metal.
The image of a monopole
Maxwell’s equations tell us that the interface conditions3 are:
- The normal component of \(\textbf{B}\) is continuous across the interface;
- the parallel component of \(\textbf{H}\) is continuous across the interface.
Inside the metal \(\textbf{H} = \textbf{B} / \mu\), \(\textbf{B}\) is finite, and so in the limit \(\mu \to \infty\) \(\textbf{H}\) vanishes. Thus, from the interface conditions, outside the metal the parallel component of \(\textbf{H}\) vanishes too. Since \(\textbf{B} = \mu \textbf{H}\) the parallel component of \(\textbf{B}\) vanishes and \(\textbf{B}\) is normal to the metal surface.

Note, that we are only interested in the field above the metal surface. It is reasonably easy to see that this field is the same as we would get were we to remove the metal and replace it with a negative image charge below the metal surface.
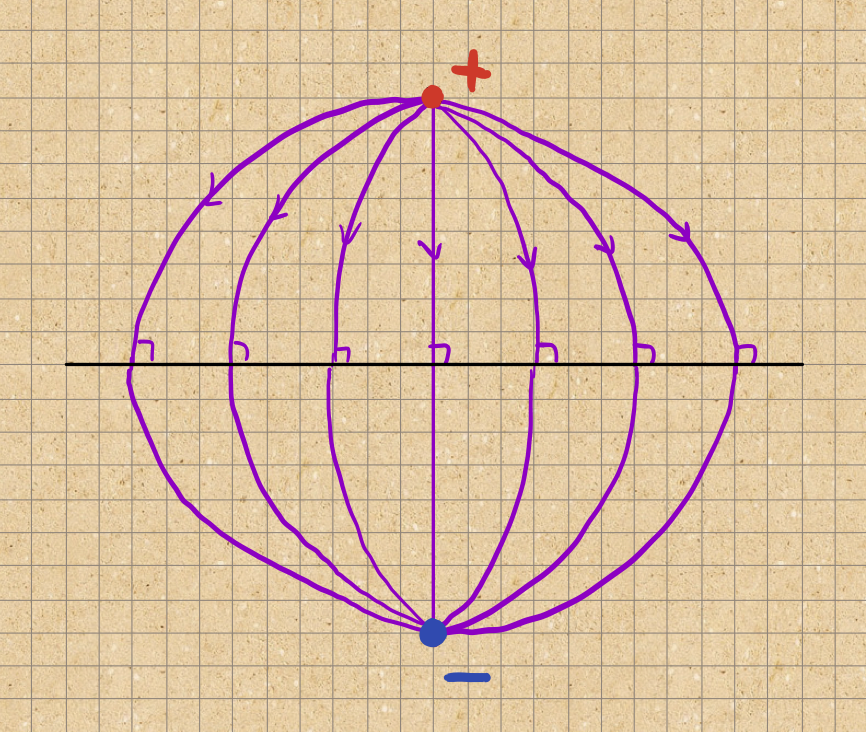
In the more general case where the field doesn’t completely vanish inside the metal, the same basic principle applies, but the algebra is more complicated.
Having a negative image charge is just like the case of an electrically-charged particle above a perfectly conducting sheet in electrostatics. Conversely, a magnetic monopole above a superconductor has an image with the same sign.
The image of a dipole
Recall that we studied the monopole because we can make a dipole by combining two monopoles. So, to work out the image of a dipole, we:
- decompose the dipole into positive and negative monopoles;
- work out the images of those monopoles;
- combine the images into an image dipole.
This is done graphically below:
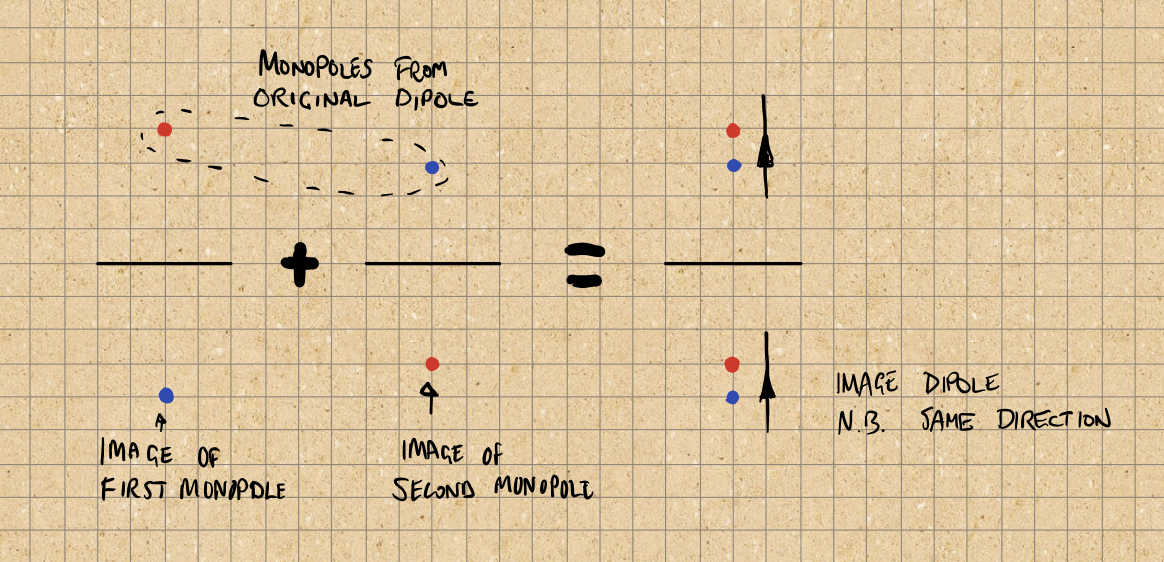
By drawing coloured dots, it is easy to see that the image of a magnetic dipole perpendicular to the surface has the same sign as the original.
This is good news, because we expect the magnet and metal to attract each other!
Incidentally, if the dipole were aligned parallel to the surface then it’s image would have the opposite sign. Happily they’d still attract though!
Getting Quantitative
Having shown how to solve the problem we now need to actually do the calculation.
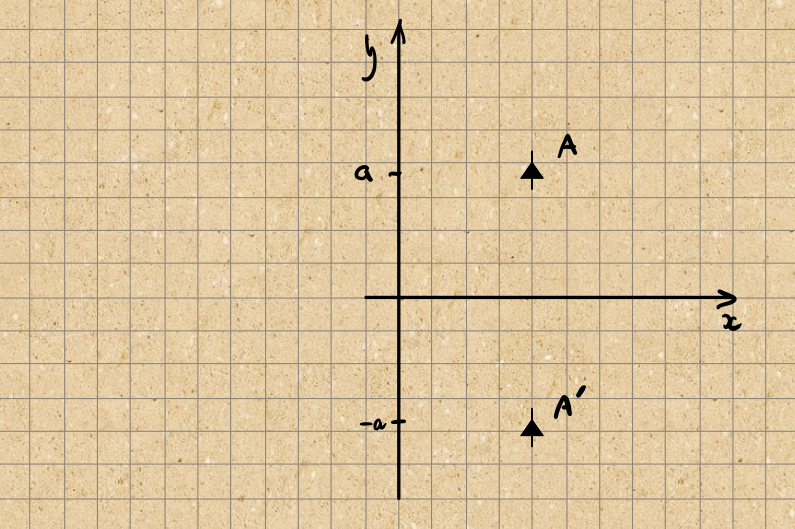
The sketch above shows the problem we’re trying to solve: what’s the force on the dipole at A due to the dipole at A' ?
The absence of currents means that we can solve the problem with a scalar potential \(\psi(\textbf{x})\). The potential seen by the dipole at A comes from the image dipole at A':
\[ \begin{align} \psi(\textbf{r}) &= \frac{\textbf{m} . \textbf{r}}{4 \pi r^3},\\\ &= \frac{m(y + a)}{4 \pi} (x^2 + (y + a)^2 + z^2)^{-3/2}. \end{align} \]From here, we can calculate the field:
\[ \textbf{H}(\textbf{r}) = - \nabla \psi. \]We only need the \(y\)-component of \(\textbf{B}\),
\[ B_y(\textbf{r}) = \frac{m \mu_0}{4 \pi} \Bigl( 3 \frac{(y + a)^2}{(x^2 + (y + a)^2 + z^2)^{5/2}} - \frac{1}{(x^2 + (y + a)^2 + z^2)^{3/2}} \Bigr), \]to calculate the force,
\[ \begin{align} \textbf{F} &= \nabla \bigl(\textbf{m} . \textbf{B} \bigr), \\\ &= m \nabla B_y, \\\ &= \frac{3 m^2 \mu_0}{4 \pi r^7} \Bigl(x \, (r^2 - 5 y'^2),\; y' \, (3 r^2 - 5 y'^2),\; z \, (r^2 - 5 y'^2)\Bigr), \end{align} \]where
\[ \begin{align} y' &= y + a, \\\ r &= x^2 + y'^2 + z^2. \end{align} \]Substituting the position of the magnet, \((x,y,z) = (0,a,0)\):
\[ \textbf{F} = \frac{3 m^2 \mu_0}{32 \pi} \Bigl( 0, -1, 0 \Bigr). \]As we’d expect, the magnet feels a force directly towards the metal.
Parallel dipoles
We could also calculate the force expected from a dipole parallel to the surface, remembering that in this case the image dipole points in the opposite direction.
The algebra is similar, so here’s the answer:
\[ \textbf{F} = \frac{3 m^2 \mu_0}{64 \pi} \Bigl( 0, -1, 0 \Bigr). \]In other words half the force we found above.
Two dipoles
Having solved simplified problem for one dipole, we can return to the real problem: two dipoles.
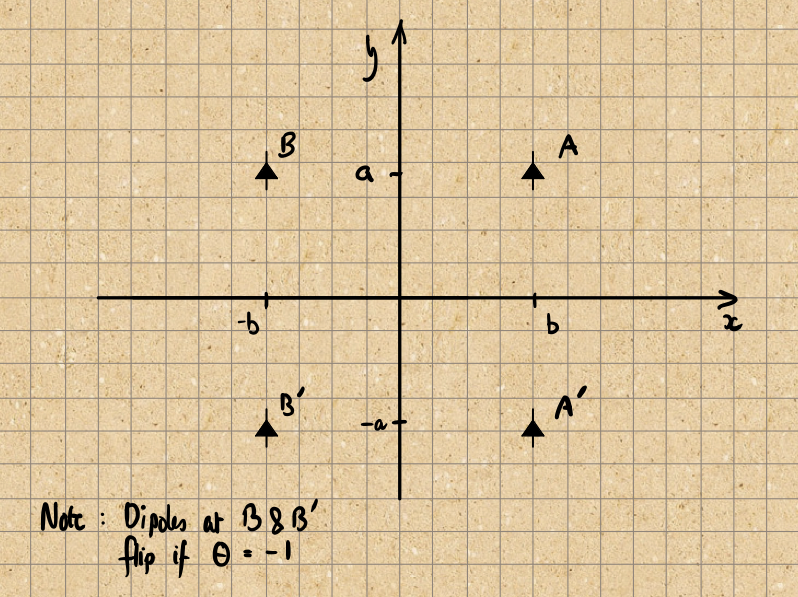
Recall the central question: how does the holding force depend on the orientation of the second dipole. Suppose that this has a dipole moment
\[ \textbf{m'} = \bigl(0, \theta m, 0 \bigr). \]The calculation proceeds as above. Introduce the short-hand for the scalar-potential from a dipole in the \(y\)-direction:
\[ \psi(x,y,z,\theta) = \frac{\theta m y}{4 \pi} \Bigl( x^2 + y^2 + z^2 \Bigr)^{-\frac{3}{2}}. \]so that we can write the total potential due to the dipoles at A' an B' as:
\[ \Psi(x,y,z) = \psi(x - b, y + a, z, 1) + \psi(x + b, y + a, z, \theta). \]Note, previously I included the potential from B here too: that’s a mistake because its position is fixed relative to A. Happily though the force turns out to be zero: it doesn’t change the calculation below.
At this point the algebra gets awfully messy, so I won’t reproduce it here. Close to the surface, we expect \(b >> a\). So, introduce
\[ \beta = \frac{a}{b}, \]noting that small \(\beta\) corresponds to widely spaced magnets.
Then we can expand in terms of \(\beta\), keeping only the first \(\beta\)-term for each component:
\[ \textbf{F} \approx \frac{3 m^2 \mu_0}{32 \pi a^4} \Bigl(\theta \beta^4, -(1 - \frac{3}{2} \theta \beta^5), 0 \Bigr). \]Three observations:
- If the magnets are aligned in the same direction they will indeed repel each other.
- The magnets will actually attract the metal more strongly if they are aligned in opposite directions.
- The effect of the interactions is pretty weak.
To quantify the last point, note that a typical magnet might have a diameter of 10mm and a thickness of 3mm, so \(\beta = 0.3\). The truncated series approximation gives:
\[ \textbf{F} \approx \frac{3 m^2 \mu_0}{32 \pi a^4} \Bigl(0.0081 \, \theta,\; -(1 - 0.0036 \, \theta),\; 0 \Bigr), \]against the exact result,
\[ \textbf{F} \approx \frac{3 m^2 \mu_0}{32 \pi a^4} \Bigl(0.0060 \, \theta,\; -(1 - 0.0025 \, \theta),\; 0 \Bigr). \]Exact here just means avoiding the error by truncating the series. It doesn’t mean that the model is faithful to reality.
Summing up
The calculation above is for one magnet, but there are of course two. Summing up the total forces:
\[ \textbf{F}_{tot} \approx - \frac{3 m^2 \mu_0}{16 \pi a^4} \Bigl(0, 1 - \frac{3}{2} \theta \beta^5, 0 \Bigr). \]To a surprisingly good approximation, two magnets hold about twice as well as one!
Conclusions
To the extent that this is a good model of reality, the pleasing conclusion is that if you’re using a couple of magnets to hold geocaches in place then putting them in opposite orientations is both easier to assemble and sticks slightly more strongly.
The more general conclusion is that when you’re using dipoles the fields and hence forces decay rapidly with distance. So, unless the magnets are really close you don’t go far wrong by ignoring this interaction.
It would be nice to verify these claims experimentally.
References
- 1. ./magnetic-bisons.html
- 2. https://en.wikipedia.org/wiki/Method_of_image_charges
- 3. https://en.wikipedia.org/wiki/Interface_conditions_for_electromagnetic_fields


![Atom Feed [ Atom Feed ]](../../atom.png)